Diamond principle
In mathematics, and particularly in axiomatic set theory, the diamond principle ◊ is a combinatorial principle introduced by Björn Jensen (1972) that holds in the constructible universe and that implies the continuum hypothesis. Jensen extracted the diamond principle from his proof that V=L implies the existence of a Suslin tree.
Contents |
Definition
The diamond principle ◊ says that there exists a ◊-sequence, in other words sets Aα⊆α for α<ω1 such that for any subset A of ω1 the set of α with A∩α = Aα is stationary in ω1.
More generally, for a given cardinal number 
and a stationary set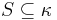 
, the statement ◊S (sometimes written ◊(S) or ◊κ(S)) is the statement that there is a sequence 
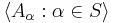such that
- each
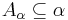
- for every
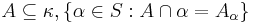is stationary in
The principle ◊ω1 is the same as ◊.
Properties and use
Jensen (1972) showed that the diamond principle ◊ implies the existence of Suslin trees. He also showed that ◊ implies the CH. Also ♣ + CH implies ◊, but Shelah gave models of ♣ + ¬ CH, so ◊ and ♣ are not equivalent (rather, ♣ is weaker than ◊).
Akemann & Weaver (2004) used ◊ to construct a C*-algebra serving as a counterexample to Naimark's problem.
For all cardinals κ and stationary subsets S⊆κ+, ◊S holds in the constructible universe. Recently Shelah proved that for κ>ℵ0, ◊κ+ follows from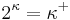 
.
See also
References
- Akemann, Charles; Weaver, Nik (2004), "Consistency of a counterexample to Naimark's problem", Proceedings of the National Academy of Sciences of the United States of America 101 (20): 7522–7525, arXiv:math.OA/0312135, doi:10.1073/pnas.0401489101, MR2057719
- Jensen, R. Björn (1972), "The fine structure of the constructible hierarchy", Annals of Mathematical lLogic 4: 229–308, doi:10.1016/0003-4843(72)90001-0, MR0309729
- Assaf Rinot, Jensen's diamond principle and its relatives, online
- S. Shelah: Whitehead groups may not be free, even assuming CH, II, Israel J. Math., 35(1980), 257–285.